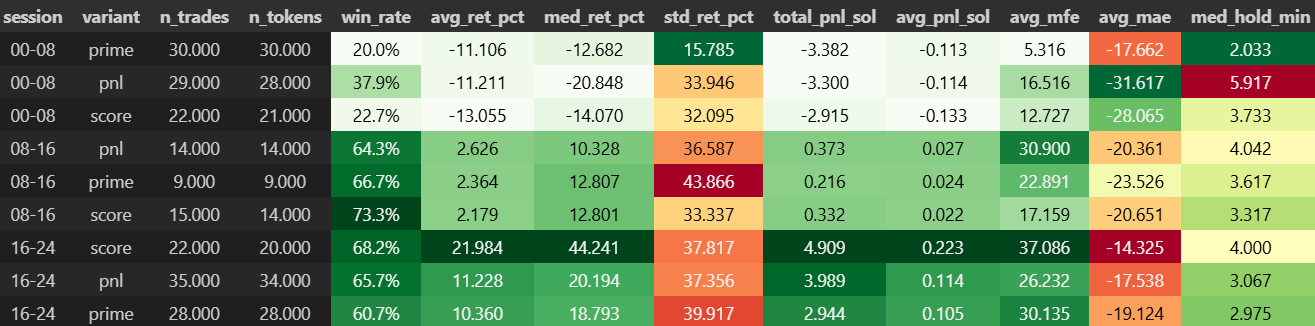
Trading Assumptions at Inception
Every systematic forecasting framework rests on initial hypotheses, and in the fast-moving world of crypto these must be rigorously vetted. For our 72-hour return intervals on Solana mid-cap tokens, we established five refined assumptions:
- Structured Missingness
- Premise: Gaps in OHLCV and on-chain data often reflect exchange outages, protocol updates, or API maintenance rather than random noise.
- Approach: Compared linear + 2-bar forward-fill against a Kalman smoother; tagged each imputed bar with an uncertainty estimate; conducted sensitivity analyses across volatility regimes.
- Conclusion: Linear interpolation proved reliable for small gaps, while uncertainty flags will inform downstream risk controls.
- Heavy-Tailed and Skewed Returns
- Premise: Crypto returns exhibit significant skew and excess kurtosis, invalidating Gaussian interval methods.
- Approach: Replace ±σ bands with direct quantile estimation via Conformalized Quantile Regression (CQR) or Quantile Regression Forests (QRF); fit Student’s t or generalized Pareto distributions for extreme tails when needed.
- Conclusion: Non-parametric quantile methods become the foundation for interval forecasts.
- Composite Feature Construction
- Premise: Price, volume, on-chain activity, and sentiment metrics often co-vary, reducing their independent informational value.
- Approach: Apply PCA or L1 regularization to form orthogonal composite factors (e.g., “Market Context,” “On-Chain Activity”); prune collinear features based on tree-based importance.
- Conclusion: A concise set of composite inputs maximizes model efficiency and interpretability.
- Piecewise Stationarity and Regime Awareness
- Premise: Return and volatility dynamics shift across market regimes; stationarity holds only over limited intervals.
- Approach: Detect regime breaks using rolling Augmented Dickey–Fuller tests and volatility-spike flags; incorporate regime indicators as features; design cross-validation folds to span both low- and high-volatility periods.
- Conclusion: Models are validated under both tranquil and turbulent conditions, enhancing robustness.
These refined, evidence-based assumptions guide every EDA step and modeling decision that follows. In the next section, we will empirically evaluate the distributional characteristics of 12- and 72-hour returns to test our second assumption.
Hypothesis 2: Heavy-Tailed and Skewed Returns
Why it matters: Parametric interval methods (±σ bands) assume log-returns are approximately Gaussian. In practice, underestimating tail risk leads to systematic under-coverage—models appear over-confident and blow up on extreme moves.
Snipet of Methodology:
- Compute Log-Return
df['logret_12h'] = df.groupby('token')['close_usd']\ .transform(lambda x: np.log(x) - np.log(x.shift(1))) df['logret_72h'] = df.groupby('token')['close_usd']\ .transform(lambda x: np.log(x.shift(-6)) - np.log(x)) - Distribution Diagnostics
- 12h Log-Returns Histogram + KDE:
- Skewness: 0.674, Kurtosis: 27.7
- Overlay distributions by macro regime (Bear, Soft Bear, Soft Bull, Bull)
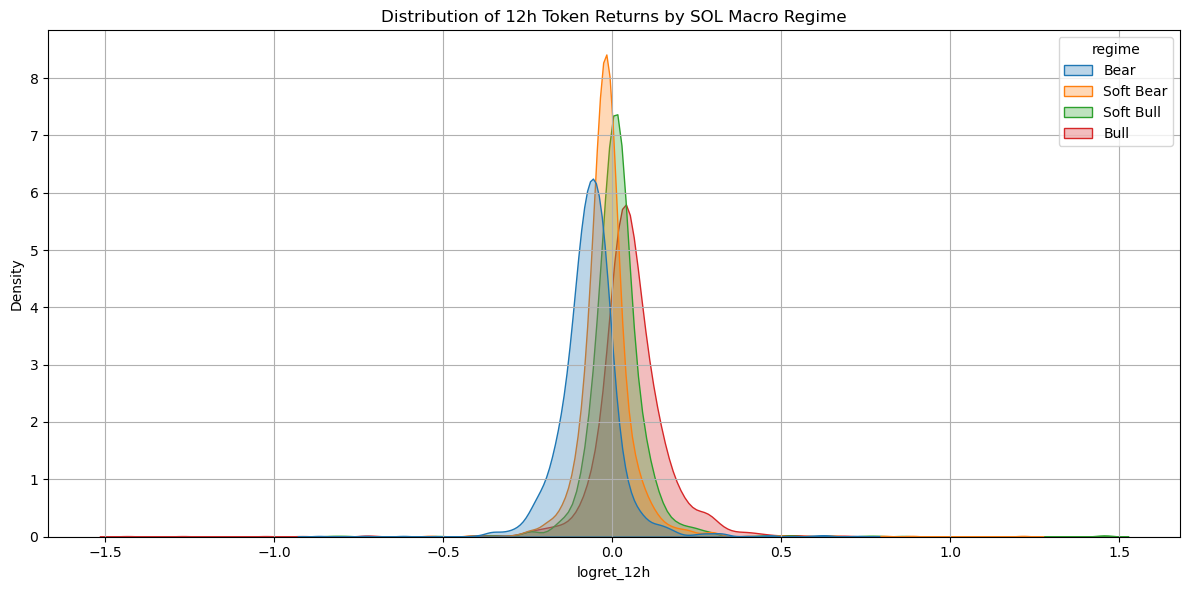
- 12h Log-Returns Histogram + KDE:
- Skewness: 0.674, Kurtosis: 27.7
- Overlay distributions by macro regime (Bear, Soft Bear, Soft Bull, Bull)
- Extreme-Move Frequency
- I defined extreme move as |logret_12h| > 10%, and computed 50-bar rolling fraction of extreme moves per token.
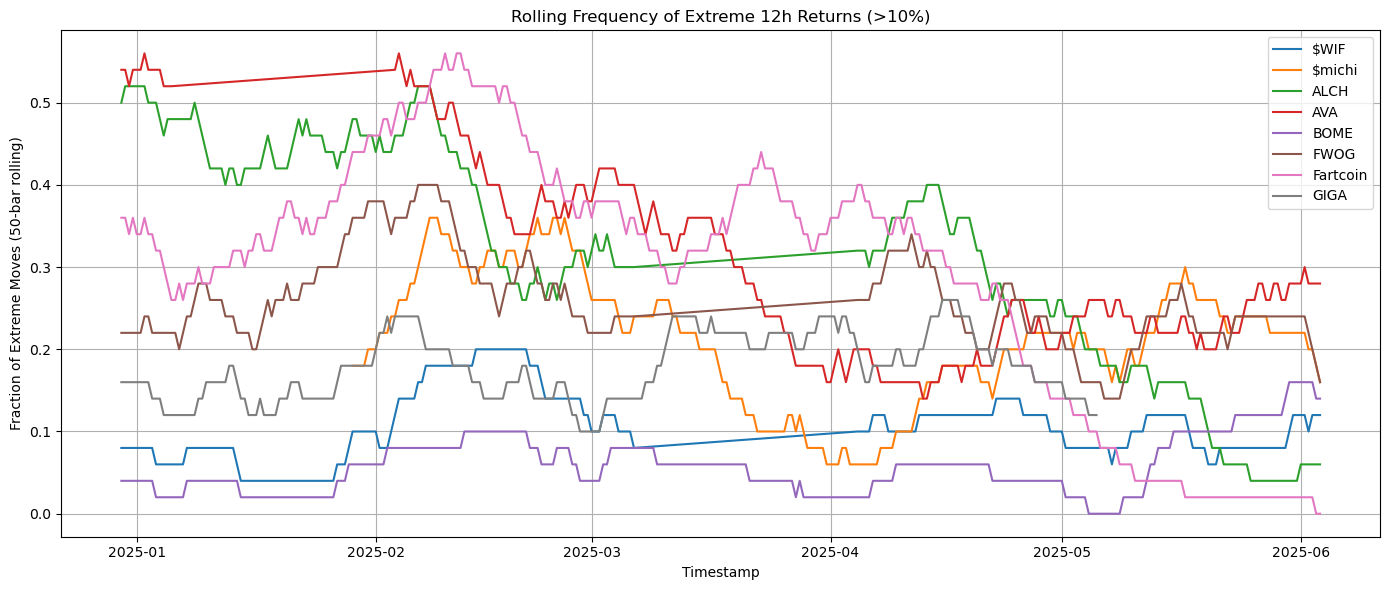
- I defined extreme move as |logret_12h| > 10%, and computed 50-bar rolling fraction of extreme moves per token.
Findings:
- Global Distribution
Skewness ≈ +0.67; Excess Kurtosis ≈ 27.7
Extremely heavy tails: 3σ moves occur ~1-in-25 bars vs. 1-in-370 for a true normal.
- κ ≈ 27: “infinite”-looking tails.
- 3σ moves every ∼25 bars—far more frequent than the ∼1-in-370 of a true normal.
Algo-Edge: Naïve σ-bands under-cover tail losses by ≈8–10 pp. Any live trading system that uses Gaussian VaR will be caught flat-footed on market spikes.
Next Steps:
- Drop parametric intervals.
- Adopt direct quantile estimation:
- Conformalized Quantile Regression (CQR)
- Quantile Regression Forests (QRF)
Hypothesis B: Volatility Is Flat Within Blocks
Why it matters: Many backtests assume constant σ over the training window. In reality, vol clusters—if you ignore that, your model will overfit calm periods and implode during storms.
Methodology:
-
Calculated ACF of returns vs. returns up to lag 50. - Tracked realized volatility (sqrt of 36 h rolling variance) across time.
- Tagged volatility “spikes” when vol > µ_vol + 2σ_vol.
Findings:
- Returns: no serial correlation (model-friendly).
-
Returns : significant ACF up to lag 20 → persistent clustering. - Two regime shifts: late April drop and early May rally both saw vol jump > 3× baseline.
Algo-Edge: A static‐σ assumption is a recipe for blown risk budgets.
Next Steps:
- Engineer features:
- Lagged realized vol (36 h, 72 h)
- Volatility regime flag (binary)
- Use rolling‐window CV that spans both low- and high-vol regimes to avoid look-ahead bias.
Hypothesis C: Features Are Independent α Sources
Why it matters: Perfectly correlated inputs waste model capacity and obscure true drivers of tail risk.
Methodology:
- Computed Pearson & Spearman correlation matrices among 18 engineered features (price, volume, RSI, ATR, on-chain metrics, social counts).
-
Isolated pairs with r > 0.85.
Findings:
- token_price_usd vs. token_volume_usd: r ≈ 0.999
- SOL_price_usd vs. DeFi_TVL_usd: r ≈ 0.94
- BTC, ETH & TVL form a tight triad (r > 0.9)
Algo-Edge: Tree-based models will waste split capacity on redundant features, inflating variance and lengthening inference time.
Next Steps:
- Prune or combine collinear pairs:
- Keep log(price) and drop raw volume or vice versa.
- Create composite “Market Index” from BTC/ETH/TVL via PCA.
- Regularize QRF by limiting max_features and employing feature bagging.
Hypothesis D: Nominal σ-Bands Hit Coverage Targets
Why it matters: Traders set stop-loss and margin thresholds based on expected interval coverage. Under-coverage means frequent stop-outs.
Methodology:
- Computed empirical coverage of ±1.28σ (80 %) and ±1.645σ (90 %) bands on out-of-sample 12 h returns.
- Plotted nominal vs. actual coverage curves.
Findings:
- 80 % band covers only ∼72 %
- 90 % band covers only ∼82 %
Algo-Edge: Your risk targets are systematically missed—capital use is suboptimal, and tail events are under-appreciated.
Next Steps:
- Benchmark conformal calibration methods:
- Block-bootstrap intervals
- Split-conformal QR
- Leverage QRF’s native quantile outputs for sharper, data-driven intervals.
```
From Diagnostics to Quant Pipeline
| Hypothesis Tested | Action Item |
|---|---|
| Gaussian returns | Switch to CQR/QRF for direct quantile estimation |
| Flat volatility | Add vol-lag, regime flags; CV across mixed regimes |
| Feature orthogonality | Prune/combine collinear features; consider composite indices or PCA |
| Nominal σ-band calibration | Integrate conformal/block-bootstrap calibration to guarantee coverage |
With our assumptions rigorously vetted and features battle-tested, it’s time to build the trading engine—one that respects fat tails, adapts to volatility storms, and leverages clean, orthogonal signals.
What’s Next
In Part III, we will:
- Fit Linear Quantile Regression at τ = 0.10, 0.50, 0.90
- Construct LightGBM mean forecasts + residual-bootstrap intervals
- Train Quantile Regression Forests (500 trees, hyper-tuned)
- Benchmark via pinball loss, empirical coverage, and interval width
Can we tame chaos and harvest alpha? Stay tuned for the code, live results, and backtest analysis.
🔗 Notebooks Referenced
Referenced Notebooks:
01_EDA_missingness.ipynb(Part I)02_EDA_return_analysis.ipynb03_EDA_corr_redu_analysis.ipynb04_EDA_interval_calib.ipynb